| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Absolute
- AGI
- ai
- AI agents
- AI engineer
- AI researcher
- ajax
- algorithm
- Algorithms
- aliases
- Array 객체
- ASI
- bayes' theorem
- Bit
- Blur
- BOM
- bootstrap
- canva
- challenges
- ChatGPT
- Today
- In Total
A Joyful AI Research Journey🌳😊
Understanding the Central Tendency in a 100-Layer Galton Board 본문
Understanding the Central Tendency in a 100-Layer Galton Board
yjyuwisely 2024. 3. 4. 07:00Q: What is the fraction of beans that end near the center (bins 40-60 among 0-100) for the ideal Galton board with 100 layers? (You may try to write a program, or use some scientific computations tool. For such a problem wolfram alpha should be enough.)
A:
The fraction of beans that end near the center (bins 40-60 among 0-100) for an ideal Galton board with 100 layers can be calculated using the properties of the binomial distribution. In an ideal Galton board, the path of each bean can be modeled as a series of independent Bernoulli trials, where each trial represents the bean falling to the left or the right at each layer.
The probability distribution of the final position of the beans follows a binomial distribution, with parameters n = 100 (the number of layers, or trials) and p = 0.5 (the probability of falling to one side at each layer, assuming the board is symmetric).
The fraction of beans ending in bins 40 to 60 can be found by summing the binomial probabilities for these outcomes. Specifically, we calculate:
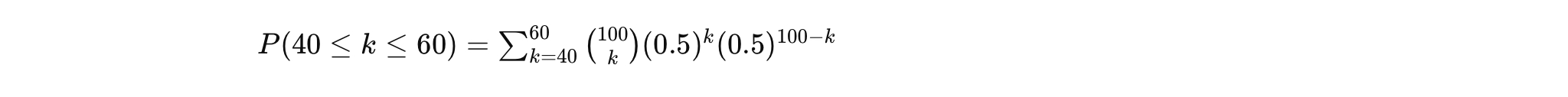
Let's compute this value now. The fraction of beans that end near the center (bins 40-60 among 0-100) for the ideal Galton board with 100 layers is approximately 0.9648, or about 96.48%.
from scipy.stats import binom # Parameters n = 100 # number of trials (layers) p = 0.5 # probability of success (falling to one side) # Summing the probabilities from 40 to 60 probability = sum(binom.pmf(k, n, p) for k in range(40, 61)) probability
Or, sum_k=40^60 (100 choose k) / 2^100 on wolfram alpha

